Cross validation is All You Need

What is Cross validation and Why Cross validation

Cross validation, sometimes called rotation validation or out-of-sample testing, is any of various similar model validation techniques for assessing how the result of a statistical analysis will generalize to an independent data set. It mainly used in where the goal is prediction and one wants to estimate how accurately a predictive model will perform in practice.

In a prediction problem, a model is usually given a dataset of known data on which training is run (training dataset), and a dataset of unknown data (or first seen data) against which the model is tested . The goal of cross-validation is to test the model’s ability to predict new data that was not used in estimating it, in order to flag problems like overfitting or selection bias and to give an insight on how the model will generalize to an independent dataset (i.e., an unknown dataset, for instance from a real problem).

When we’re building a machine learning model using some data, we often split our data into training and validation/test sets. The training set is used to train the model, and the validation/test set is used to validate it on data it has never seen before. The classic approach is to do a simple 80%-20% or 70%-30% split. But in cross-validation, we do more than one split. We often do 3, 5, 10 or any K number of splits. Those splits called Folds, and there are many strategies we can create these folds with.

It is necessary to make it clear that, the aim of cross validation it not to get one or multiple trained models for inference, but to estimate an unbiased generalization performance. In this way, we can tuning the model’s hyper-parameter based on cross validation results.

Another thing needed to be noted is that we have to separate “hyper parameter tuning” and “model evaluation” by using two two test set for each task.

Type of Cross validation

Simple K-Folds Cross validation

In K Fold cross validation, the data is divided into k subsets. Now the holdout method is repeated k times, such that each time, one of the k subsets is used as the test set/ validation set and the other k-1 subsets are put together to form a training set. The error estimation is averaged over all k trials to get total effectiveness of our model.

As can be seen, every data point gets to be in a validation set exactly once, and gets to be in a training set k-1 times. This significantly reduces bias as we are using most of the data for fitting, and also significantly reduces variance as most of the data is also being used in validation set. Interchanging the training and test sets also adds to the effectiveness of this method. As a general rule and empirical evidence, K = 5 or 10 is generally preferred, but nothing’s fixed and it can take any value.

Leave One Out

This approach leaves p data points out of training data, i.e. if there are n data points in the original sample then, n-p samples are used to train the model and p points are used as the validation set. This is repeated for all combinations in which original sample can be separated this way, and then the error is averaged for all trials, to give overall effectiveness.

A particular case of this method is when p = 1. This is known as Leave one out cross validation. This method is generally preferred over the previous one because it does not suffer from the intensive computation, as number of possible combinations is equal to number of data points in original sample or n.

Stratified K-Folds Cross-validation

In some cases, there may be a large imbalance in the response variables. For example, in dataset concerning price of houses, there might be large number of houses having high price. Or in case of classification, there might be several times more negative samples than positive samples. For such problems, a slight variation in the K Fold cross validation technique is made, such that each fold contains approximately the same percentage of samples of each target class as the complete set, or in case of prediction problems, the mean response value is approximately equal in all the folds. This variation is also known as Stratified K Fold.

Above explained validation techniques are also referred to as Non-exhaustive cross validation methods. These do not compute all ways of splitting the original sample, i.e. you just have to decide how many subsets need to be made. Also, these are approximations of method explained below, also called Exhaustive Methods, that computes all possible ways the data can be split into training and test sets.

How to do Hyper-parameter tuning and model evaluation at the same time

Nested Cross validation

When doing one round CV to evaluate the performance of different models, and select the best model based on the CV results, it is using test set both for model selection and estimation, which will cause “information leaking”. Thus, when we want to perform model selection and generalization error estimation, we have to separate the two tasks by using two test set for each task. That’s why we have the validation and test set, and the same version in CV is called nested or two-round cross validation.

The nested CV has an inner loop CV nested in an outer CV. The inner loop is responsible for model selection/hyper-parameter tuning (similar to validation set), while the outer loop is for error estimation (test set).

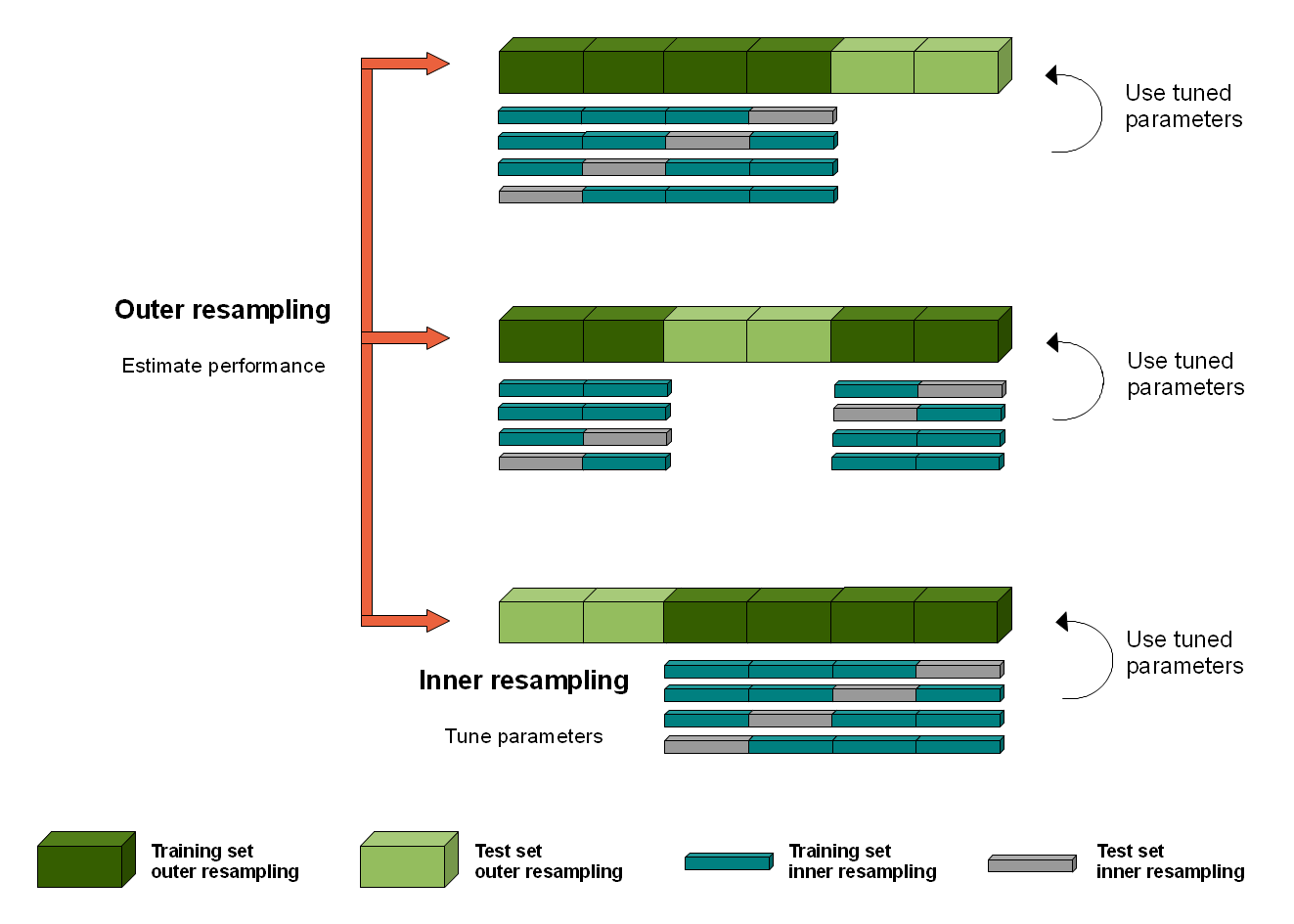
Single-Loop Cross validation

However, Nested Cross validation will a large computation cost. For example, if we use 5-Folds cross validation for both outer and inner loop, the entire validation process need to 5*5 round to finish, which is time and computation cost. Thus, for simplify, we can use Single-loop Cross validation.

The Single-Loop Cross-validation only has an outer CV, but in each round of outer CV, we perform simple data split to get train data and validation instead of inner cross validation. The train set were used to trained the model and hyper-parameter tuning were performed on validation. After model training and tunning, the final performance is evaluated on the test set.

Recommend Strategies

We performed nested cross-validation to tune model hyper-parameter and evaluate model performance. The nested cross-validation has an inner loop cross-validation nested in an outer cross-validation. The inner loop is responsible for model selection/hyper-parameter tuning (similar to validation set), while the outer loop is for error estimation (test set). In the inner loop (here executed by grid search with stratified 5-fold cross validation), the score is approximately maximized by fitting a model to each training set, and then directly maximized in selecting (hyper)parameters over the validation set. In the outer loop (stratified 5-fold cross validation), generalization performance (AUC in our work) is estimated by averaging test set scores over several dataset splits. We repeated the whole nested cross-validation process 3,000 times.

Sklearn API for Cross-Validation

Sklearn provide several cross-validation approach in Model Selection section

Splitter Classes

Hyper-parameter optimizers

Reference

[1] T. Hastie, J. Friedman, and R. Tibshirani, “Model Assessment and Selection,” in The Elements of Statistical Learning: Data Mining, Inference, and Prediction, T. Hastie, J. Friedman, and R. Tibshirani, Eds. New York, NY: Springer New York, 2001, pp. 193–224.

[2] G. C. Cawley and N. L. C. Talbot, “On Over-fitting in Model Selection and Subsequent Selection Bias in Performance Evaluation,” Journal of Machine Learning Research, vol. 11, no. Jul, pp. 2079–2107, 2010.

[3] 5 Reasons why you should use Cross-Validation in your Data Science Projects

[4] Cross-Validation in Machine Learning

[5] A Gentle Introduction to k-fold Cross-Validation (machinelearningmastery.com)

[6] What is the purpose of performing cross-validation? (researchgate.net)

[7] Cross-validation (statistics) - Wikipedia