怎么知道你建立的人工智能分类模型就是靠谱的？

使用人工智能算法开发的基于的风险预测模型的预后研究是我研究生以来主要研究的课题。在阅读文献和自己实验过程中，发现各种各样的预测模型质量参差不齐，评价指标又纷繁复杂，那么如何去评价一个模型的好坏，或者说当你构建出一个人工智能疾病风险预测模型后，它到底靠不靠谱，能不能说服审稿人和读者，值不值得去推广和使用呢？这是一个我们需要去好好考量的问题。

一个好的疾病风险预测模型，它能够把未来发病风险高、低不同的人群正确地区分开来，预测模型通过设置一定的风险界值，高于界值判断为发病，低于界值则判断为不发病，从而正确区分个体是否会发生结局事件，这就是预测模型的区分度 (Discrimination)。

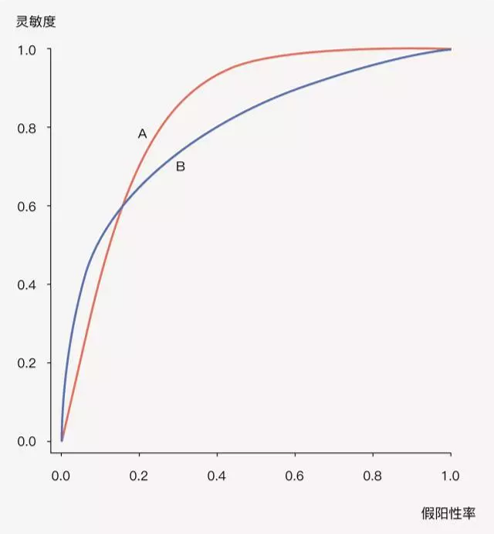
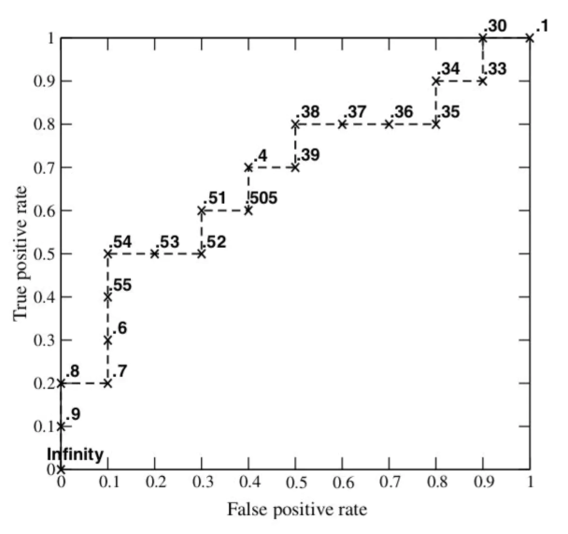
评价预测模型区分能力的指标，最常用的就是大家非常熟悉的ROC曲线下面积（AUC），也叫C统计量（C-statistics）。AUC越大，说明预测模型的判别区分能力越好。一般AUC<0.6认为区分度较差，0.6-0.75认为模型有一定的区分能力，>0.75认为区分能力较好。

AUC 理解与计算

AUC 的全称是 AreaUnderRoc 即 Roc 曲线与坐标轴形成的面积，取值范围 [0, 1].

ROC

Roc (Receiver operating characteristic) 曲线是一种二元分类模型分类效果的分析工具。首先需要知道如下定义：

Roc 空间将伪阳性率(FPR)定义为 X 轴，真阳性率(TPR)定义为 Y 轴。

  • TPR: 在所有实际为阳性的样本中，被正确地判断为阳性之比率 TPR = TP/P = TP/(TP+FN)
  • FPR: 在所有实际为阴性的样本中，被错误地判定为阳性之比率 FPR = FP/N = FP/(FP + TN)

给定一个二元分类模型和它的阈值，就能从所有样本的（阳性／阴性）真实值和预测值计算出一个 (X=FPR, Y=TPR) 座标点。

绘制完成的ROC曲线
ROC曲线绘制步骤

Calibration plot 校准度曲线

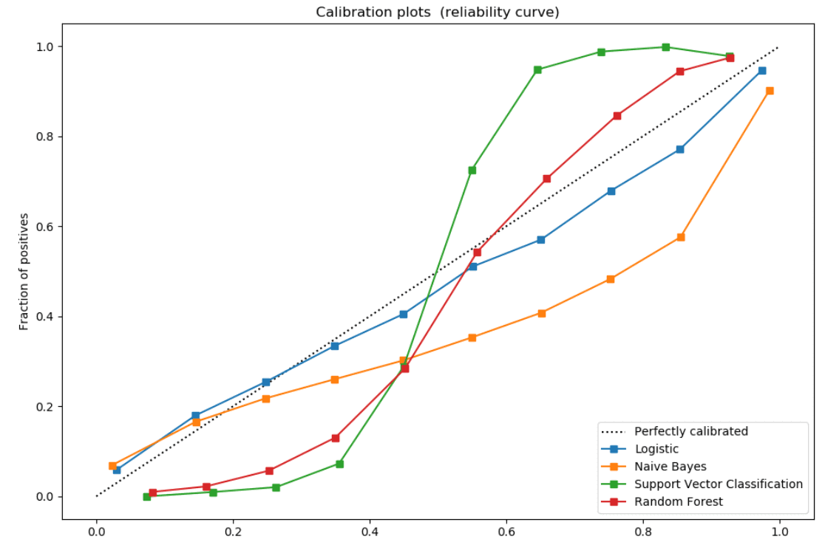
预测模型的校准度(Calibration)，是评价一个疾病风险模型预测未来某个个体发生结局事件概率准确性的重要指标，它反映了模型预测风险与实际发生风险的一致程度，所以也可以称作为一致性。

校准度好，提示预测模型的准确性高，校准度差，则模型有可能高估或低估疾病的发生风险。

横坐标是模型预测出来为阳性的概率，纵坐标是真正阳性的概率。如果预测结果是没有偏差的，模型应该和虚线重合。

校准度曲线绘制步骤

1、对分类器的预测概率从大到小进行排序；

2、使用等频或者等宽分箱，一般为10等分；

3、计算每一个箱子中的预测概率的均值和真实概率（根据这个箱子里的样本的实际的标签来计算），比如二分类问题，取样本标签为1的概率，某个箱子的概率区间是0~0.1，则预测概率的均值简单假设是0.05，表示处于这个区间的样本中，假设有100个样本则实际应该有5个样本属于类别1，而实际的这个区间中的样本，假设有100个，而实际上有10个属于类别1，此时我们就称概率发生了偏误。

4、分箱之后，横坐标是每个箱子的预测概率的均值，纵坐标是每个箱子的实际上的预测概率。

5、图中的斜虚线表示预测概率完全符合真实概率的情形

Calibration curve

Net classification improvement (NRI) 净重新分类改善指数

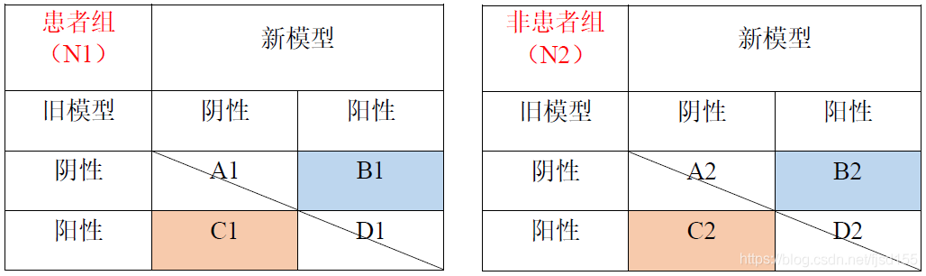
相对于AUC，NRI更关注在某个设定的切点处，两个模型把研究对象进行正确分类的数量上的变化。简单的说，首先旧模型会把研究对象分类为患者和非患者，然后在旧模型的基础上引入新的指标构成新模型，新模型会把研究对象再重新分类成患者和非患者。

此时比较新、旧模型对于研究人群的分类变化，就会发现有一部分研究对象，原本在旧模型中被错分，但在新模型中得到了纠正，分入了正确的分组，同样也有一部分研究对象，原本在旧模型中分类正确，但在新模型中却被错分，因此研究对象的分类在新、旧模型中会发生一定的变化，我们利用这种重新分类的现象，来计算净重新分类指数NRI。

我们主要关注被重新分类的研究对象，从表中可以看出，在患者组（总数为N1），新模型分类正确而旧模型分类错误的有B1个人，新模型分类错误而旧模型分类正确的有C1个人，那么新模型相对于旧模型来说，正确分类提高的比例为(B1-C1) / N1，即对角线以上的比例-对角线以下的比例。

同理，在非患者组（总数为N2），新模型分类正确而旧模型分类错误的有C2个人，新模型分类错误而旧模型分类正确的有B2个人，那么新模型相对于旧模型正确分类提高的比例为(C2-B2) / N2，即对角线以下的比例-对角线以上的比例。

最后，综合患者组和非患者组的结果，新模型与旧模型相比，净重新分类指数NRI= (B1-C1) / N1+(C2-B2) / N2

若NRI＞0，则为正改善，说明新模型比旧模型的预测能力有所改善；若NRI＜0，则为负改善，新模型预测能力下降；若NRI=0，则认为新模型没有改善。

Net classification improvement

Integrated discrimination improvement (IDI) 重分类改善指标

•在诊断试验中，我们比较两个模型的优劣时，除了可以比较两个模型ROC曲线下面积外，还可以用定量的指标来比较一个模型比另外一个模型诊断准确率改进的程度。我们介绍过NRI（Net Reclassification Improvement，重分类改善指标），NRI定量地表示一个指标在某界值下的诊断准确率比另一指标准确率提高多少，容易理解，也比较容易计算。缺点是只考虑了界值时的情况，同时另外一个指标可以弥补这个不足，即IDI。

•IDI（Integrated Discrimination Improvement，综合判别改善指数）也是Pencina等人于2008年提出的，它使用模型（或指标）对每个个体的预测概率计算得到，计算方法为： \(IDI = (P_{new,events}-P_{old, events}) - (P_{new,non-events}-P_{old, non-events})\) 其中$P_{new, events}$、$P_{old,events}$表示在患者组中，新模型和旧模型对于每个个体预测疾病发生概率的平均值，两者相减表示预测概率提高的变化量，对于患者来说，预测患病的概率越高，模型越准确，因此差值越大则提示新模型越好。

而$P_{new, non-events}$、$P_{old,non-events}$表示在非患者组中，新模型和旧模型对于每个个体预测疾病发生概率的平均值，两者相减表示预测概率减少的量，对于非患者来说，预测患病的概率越低，模型越准确，因此差值越小则提示新模型越好。

最后，将两部分相减即可得到IDI，总体来说IDI越大，则提示新模型预测能力越好。与NRI类似，若IDI＞0，则为正改善，说明新模型比旧模型的预测能力有所改善，若IDI＜0，则为负改善，新模型预测能力下降，若IDI=0，则认为新模型没有改善。